컴퓨터 그래픽스를 OpenGL로 구현하기 위해서는 선형대수학을 알아야한다.
목차는 다음과 같다.
▪ 행렬과 벡터
▪ 좌표와 기저
▪ 내적
▪ 벡터곱
▪ 직선 및 선형 보간
행렬이란, 숫자들을 직사각형 형태로 행과 열에 따라 나열한 것을 칭한다.
다음과 같이 표현한다.

행렬 곱 공식

그러니까 3x2 행렬과 2x3 행렬을 곱하면 아래처럼 된다.
c(1,1) = a(1,1)*b(1,1) + a(1,2)*b(2,1)
c(1,2) = a(1,1)*b(1,2) + a(1,2)*b(2,2)
c(1,3) = a(1,1)*b(1,3) + a(1,2)*b(2,3)
c(2,1) = a(2,1)*b(1,1) + a(2,2)*b(2,1)
c(2,2) = a(2,1)*b(1,2) + a(2,2)*b(2,2)
c(2,3) = a(2,1)*b(1,3) + a(2,2)*b(2,3)
c(3,1) = a(3,1)*b(1,1) + a(3,2)*b(2,1)
c(3,2) = a(3,1)*b(1,2) + a(3,2)*b(2,2)

벡터란
1) 행 또는 열의 크기가 1인 행렬을 말한다.
열 형태로 표현하면 열벡터라고 칭한다.

2) 벡터 공간의 원소를 말한다.
벡터공간은
컴퓨터 그래픽스를 OpenGL로 구현하기 위해서는 선형대수학을 알아야한다.
행렬이란, 행과 열로 구성되며 다음과 같이 표현한다.

행렬 곱 공식

그러니까 3x2 행렬과 2x3 행렬을 곱하면 아래처럼 된다.
c(1,1) = a(1,1)*b(1,1) + a(1,2)*b(2,1)
c(1,2) = a(1,1)*b(1,2) + a(1,2)*b(2,2)
c(1,3) = a(1,1)*b(1,3) + a(1,2)*b(2,3)
c(2,1) = a(2,1)*b(1,1) + a(2,2)*b(2,1)
c(2,2) = a(2,1)*b(1,2) + a(2,2)*b(2,2)
c(2,3) = a(2,1)*b(1,3) + a(2,2)*b(2,3)
c(3,1) = a(3,1)*b(1,1) + a(3,2)*b(2,1)
c(3,2) = a(3,1)*b(1,2) + a(3,2)*b(2,2)

벡터란? 행 또는 열의 크기가 1인 행렬을 말한다.
열 형태로 표현하면 열벡터라고 칭한다.

행렬의 곱을 알아 보겠다

3x2과 2x1 행렬을 곱해보자

3x1 크기가 되고 행렬곱 공식에서 급수는 n이 된다
c(1,1) = a(1,1)*b(1,1) + a(1,2)*b(2,1) = ax + by
c(2,1) = a(2,1)*b(1,1) + a(2,2)*b(2,1) = cx + dy
c(3,1) = a(3,1)*b(1,1) + a(3,2)*b(2,1) = ex + fy
행렬의 좌표에서, 행과 열을 바꾸면 그것을 전치 행렬이라고 함.

표기 기호는 아래와 같음

아래처럼 계산식을 전치시키면 결과도 전치행렬로 바뀜.

행렬 벡터 곱셈을 어떻게 표현하는가의 차이이다.
Open GL은 좌측 같은 열벡터를 사용한다.
Direct 3D는 우측 같은 행벡터를 사용한다.
행과 열의 크기가 같으면 정사각 행렬이라고 함. (아니면 정방행렬)
정사각 행렬에서 왼쪽 끝과 오른쪽 아래를 잇는 대각선에 놓인 원소가 전부 1이고 나머지가 전부 0이면
단위 행렬이라고 함
1 0
0 1
1 0 0
0 1 0
0 0 1
이런 것임
특이사항으로 단위행렬 I과 다른 행렬 M을 곱하면, 결과는 기존의 M과 동일함

역행렬은 행렬 A와 곱해서 항등행렬이 되는 행렬이다.
특징 첫번째,
두 행렬의 곱의 결과가 단위행렬이면 두 행렬 중 하나는 나머지 하나의 역행렬이다.
두번째, 행렬 A와 A의 역행렬의 곱은 단위행렬이다.
식으로 표현하자면 아래와 같다.

항등행렬은 정사각형 행렬로, 주대각선의 모든 원소가 1이고 나머지 원소가 0인 행렬입니다.
2x2 항등행렬의 예는 아래와 같다.

벡터 공간이란, 벡터 덧셈과 스칼라 곱셈이 정의된 집합으로, 이 두 연산이 교환법칙, 결합법칙, 분배법칙, 항등원과
역원의 존재 등의 공리를 만족하는 구조입니다.
예를 들어, 아래는 n차원 실수 벡터들로 이루어진 벡터 공간을 나타냅니다.

벡터공간 V의 임의의 벡터 v ∈ V에 대해"라는 표현은 "벡터공간 V에 속하는 모든 벡터 v에 대하여"
라는 뜻이다.
항등원이란, 벡터공간 V에서 모든 벡터 성립하는 유일한 벡터 0∈V를 의미합니다.
(주의, 0은 정수 0이 아니고 항등원을 칭하는 기호임)

벡터 덧셈의 항등원의 모든 원소는 항상 0이고
벡터 곱셉의 항등원은 항상 단위행렬이다
항등원에 관한 성질 두가지를 알아보겠다.
역원이란, 벡터공간 V의 임의의 벡터 v∈V에 대해, v의 역원은 v + (-v) = 0를 만족하는
유일한 벡터 -v∈V를 의미합니다.

벡터공간 V의 공리는 10가지가 있으나 4가지만 살펴보자면 아래와 같습니다.



벡터의 길이는 아래처럼 표현한다.

그리고 이렇게 구한 벡터의 길이로 벡터를 나누는 과정을 정규화라고 한다.
식으로 표현하자면 아래와 같다.

정규화를 통해서 만들어진 벡터는 항상 1이며 이를 단위 벡터라고 부른다.
선형결합이란?

그러니까 요약하자면 모두 더하는 행위라고 보면 됩니다.
선형성이란 어떤 연산이나 함수가 덧셈과 스칼라 곱을 보존하는 성질을 말한다.
(선형결합과 선형성은 아예 무관하니 주의해야합니다. 선형결합은 그냥 '결합'이라고 봐도
됩니다.)
선형독립

인 상태입니다.
다른 말로는, 선형 결합으로 이뤄진 식에서 모든 벡터의 계수가 0인 상황을 칭한다. 라고 할 수 있습니다.
선형종속
위 식에서 스칼라가 0이 아니여도

기저란 벡터 공간의 모든 벡터를 최소한의 선형결합으로 표현할 수 있게 해주는 벡터 집합

2차원 평면 R^2에서 임의의 벡터 v = (x,y)는

로 표현되므로, (1, 0)과 (0,1)은 2차원 공간의 기저입니다.
표준 기저란 2차원 공간 R^2에서 각 축의 길이가 1인 단위 벡터이다.
수학적 표현 양식으로는 이렇다.

예시로, 임의의 벡터 v = (3, -2)는 표준 기저를 사용하여
v=3e1-2e2로 표현이 된다.

비표준기저라는 것도 있다. 표준기저(예 : (1,0) (0,1)가 아닌, 임의로 선택된 선형 독립 벡터들의 집합
이다.
좌표계는 원점과 기저로 정의가 된다.
그래픽스에서는 좌표계를 공간으로도 부른다.
그림으로는 아래처럼 표현을 한다.

직교란 두 벡터가 서로 수직인 상태를 의미합니다.
덧붙여서 두 벡터 u와 v가 직교하려면 uㆍv = 0을 만족해야합니다
그것을 내적이 0이다 라고도 합니다.
내적이란, 두 벡터를 곱해서 벡터의 길이(노름)을 얻는 연산과정을 칭합니다.
기호는 ㆍ입니다.
벡터 연산은 내적, dot product, inner product라고도 표현을 함
벡터의 좌표 정의가 아래 일때

벡터는 두가지 내적 방식으로 정의를 할 수 있습니다.
좌표적 정의는 아래처럼 표현하는 방식을 칭합니다. (노름을 구하는 공식으로도 볼 수 있습니다)

기하학적 정의는 아래처럼 표현하는 방식을 칭합니다. ( (노름을 구하는 공식으로도 볼 수 있습니다)

두 방식은 사실 같은 것을 다르게 표현하는 것입니다.
덧붙여서, 자기 자신끼리 내적하면 1이 되고

다른 벡터끼리 내적하면 0이 된다

내적의 결과가 음수면 둔각임

정규 또는 단위 벡터란 벡터의 길이 또는 노름이 1인 벡터를 의미합니다.
||v|| 이렇게 표현하고 ||v||=1 이렇게도 표현 가능함.
정규 (또는 단위벡터 또는 정규 벡터)인지 알아내는 방법은 길이를 구하면 됨.
예를들어 단위 벡터 e1 = (1,0)의 길이는 ||e1|| = (1^2+0^2)^(1/2)=1임

표준기저는 각 좌표축을 따라가는 단위 벡터들로 이루어진 기저를 말한다
다른 벡터를 표현하는데에 유용하게 사용됨
예를들어 (3,5)라는 벡터를 얻으려면?
(e1,e2)를 (3,5)로 변환하고자 해야한다
그럼 우선 e1,e2로 하나의 벡터를 만들어야 하기 떄문에 두개를 더하는 꼴인
e1 + e2가 된다 그리고 크기를 맞추기 위해 스칼라를 곱해서 3e1 + 5e2
실좌표로 변환 3(1,0) + 5(0,1) = (3,0)+(0,5)=(3,5)가 된다
아 참고로 표준기저 말고 비표준기저로 표현할 수 있다
비표준기저란 단위벡터가 아닌 사용자가 임의로 정의한 벡터로 이루어진 기저를 말한다.
차이를 그래프로 보자면 이렇다.

선형대수에서 해는 자명한 해와 자명하지 않은 해로 나뉜다. 자명한 해는
션형결합 식에서 모든 계수가 0인 경우고, 자명하지 않은 해는 모든 벡터들 중
계수가 하나라도 0이 아니면 자명하지 않은 해라고 한다. 근데 하나라도 0이 아니니까 이
식은 이제 선형독립이 아닌 선형 종속이다.
참고로 벡터가 3개면 3차원 공간이 된다.

두 개의 n차원 벡터를 a와 b로 표현을 하면 (a1, a2, ... , an) (b1, b2, ... bn) 이런 식으로
각 좌표를 정의를 할 수 있습니다
벡터 곱은 주로 R^3 (3차원 공간)에서만 다룹니다.
벡터 곱이란 두 벡터에 모두 수직인 새로운 3차원 벡터이며, a × b로 표현한다.
이것을 구하는 공식은 ||a × b|| = ||a|| ||b|| sin θ 이다.
내적 공식과의 차이점으로, 내적은 sin 대신 코사인을 쓴다는 것이다.

이때, a벡터와 b벡터를 변으로 삼는 평행사변형의 넓이가 새로운 벡터 (= a × b)와 동일하다.
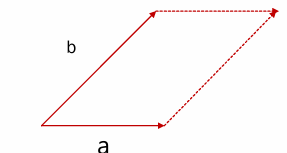
여기서 밑면은 ||a||, 높이는 ||b||, 각도는 sin θ이다.
만약 벡터 곱을 a × b 이 아닌 b × a로 정의한다면 아래처럼 길이는 같지만
방향은 반대로 바뀌어서 마이너스로 표현한다.

이러한 성질을 반가환적이라고 부른다.
보간이란? 이미 알려진 두 데이터 사이의 측정되지않은 값을 추정하여 채우는 과정이다.
선형 보간이란? 두 점 사이의 값을 직선을 기준으로 추정하거나 계산하는 방법이다.
두 점 사이의 직선을 따라가는 점 p(t)를 식으로 표현할 수 있다.
p(t) = (1 - t)p₀ + tp₁
- p₀, p₁: 양 끝 점 (시작점, 끝점)
- t: 0에서 1 사이의 보간 값
- p(t): t 값에 따라 p₀에서 p₁ 사이의 어느 점
t = 0이면 p(t) = p₀ (시작점)
t = 1이면 p(t) = p₁ (끝점)
t = 0.5이면 p(t)는 p₀와 p₁의 중간점
p(t)의 식이 위와 같은 이유는 t = 0일 때 p₀, t = 1일 때 p₁이 되게 하려는 목적이다. p₀와 p₁ 사이를 "비율"로 섞은 것이라고
보면 된다.
p(t)=p0+t(p1−p0)
이렇게도 표현 가능하다.
그냥 단순하게 시작점 + 보간비율 * 간격이라고 보면 된다.

- 조건 : A (2, 1) B (7, 4) C (4.9, y)
▶ 해결 과정:
- x축에서 A~B 사이의 거리 = 7 - 2 = 5
- A~C 거리 = 4.9 - 2 = 2.9
- 따라서 전체 거리 중 C가 차지한 비율:2.95=0.58\frac{2.9}{5} = 0.58
- 이 0.58을 선형 보간의 비율 t로 사용
- A의 y값: 1
- B의 y값: 4
→ y 변화량 = 4 - 1 = 3 - 비율 t = 0.58일 때, y는:1+0.58×3=1+1.74=2.741 + 0.58 \times 3 = 1 + 1.74 = 2.74
✅ 최종 결과:
- 점 C의 좌표는 (4.9, 2.74)
'Other > Computer Graphics' 카테고리의 다른 글
| 컴퓨터 그래픽스 4주차 : 진효진 (0) | 2025.03.31 |
|---|---|
| 컴퓨터 그래픽스 3주차 (1) | 2025.03.24 |
| 컴퓨터 그래픽스 1주차 - 최지현 교수님 (0) | 2025.03.10 |

댓글